Answer:
D
Explanation:
So we have the function:
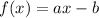
And we want to find its inverse.
To find the inverse of a function, we need to: 1) change f(x) and x, 2) change f(x) to f⁻¹(x), and 3) solve for f⁻¹(x) for the inverse.
So, flip f(x) and x:
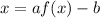
Change:
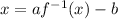
Solve. Add b to both sides. The right side cancels:
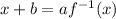
Divide both sides by a:
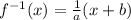
So, our answer is D.