Question

Please can someone answer this for me, ive asked so many questions on here and they never get answered, I need the help rn this is like the last thing I can think of

Given f(x) = ax – b, what is f-1(x)?
A) x - b a
B) x + b a
C) 1 ax - b
D) 1 ax + b

Answer 1

D

Explanation:

So we have the function:

`f(x)=ax-b`

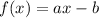
And we want to find its inverse.

To find the inverse of a function, we need to: 1) change f(x) and x, 2) change f(x) to f⁻¹(x), and 3) solve for f⁻¹(x) for the inverse.

So, flip f(x) and x:

`x=a{f(x)-b`

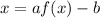
Change:

`x=a {f^(-1)(x)-b`

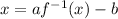
Solve. Add b to both sides. The right side cancels:

`x+b=a{f^(-1)(x)`

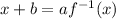
Divide both sides by a:

`f^(-1)(x)=(1)/(a)(x+b)`

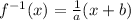
So, our answer is D.