Question

The half life of Carbon-14 is 5730 years. You measure a rock sample and find that it has trace amounts of Carbon-14. 1/2408 remains. How old is the rock?

Answer 1

Given :

The half life of Carbon-14 ,
`t_(0.5)=5730` .

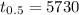Trace amounts of Carbon-14 1/2408 remains.

To Find :

How old is the rock .

Solution :

Let , initial concentration of Carbon-14 is C .

Quantity remains ,
`(C)/(2408)` .

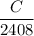Rate constant is :

`k=(0.693)/(t_(0.5))\\\\k=(0.693)/(5730)\\\\k=1.2* 10^(-4)\ years^(-1)`

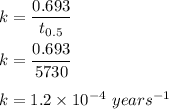
By first order equation :

`kt=-ln(([A_t])/([A_o]))\\\\t=-(ln(([A_t])/([A_o])))/(k)\\\\t=-(ln(([A_o])/([A_o]* 2408)))/(1.2* 10^(-4))\ years\\\\t=-(ln((1)/(2408)))/(1.2* 10^(-4))\ years\\\\t=64887.9\ years`

Therefore , the rock is 64887.9 years old .

Hence , this is the required solution .