Given :
The half life of Carbon-14 ,
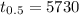 .
.
Trace amounts of Carbon-14 1/2408 remains.
To Find :
How old is the rock .
Solution :
Let , initial concentration of Carbon-14 is C .
Quantity remains ,
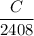 .
.
Rate constant is :
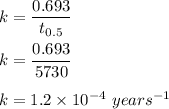
By first order equation :
![kt=-ln(([A_t])/([A_o]))\\\\t=-(ln(([A_t])/([A_o])))/(k)\\\\t=-(ln(([A_o])/([A_o]* 2408)))/(1.2* 10^(-4))\ years\\\\t=-(ln((1)/(2408)))/(1.2* 10^(-4))\ years\\\\t=64887.9\ years](https://img.qammunity.org/2021/formulas/biology/high-school/2di77ppqvbwytfl5pywjywc4oony53cmqy.png)
Therefore , the rock is 64887.9 years old .
Hence , this is the required solution .