The projectile is fired with speed
 at an angle
at an angle
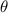 relative to the horizontal, so that the horizontal components of the initial velocity vector are
relative to the horizontal, so that the horizontal components of the initial velocity vector are
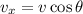
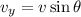
Its position vector has components
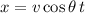
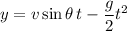
where
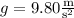
Recall that
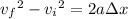
where
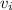 and
and
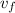 are the projectile's initial and final velocities,
are the projectile's initial and final velocities,
 is its acceleration, and
is its acceleration, and
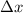 is its displacement.
is its displacement.
In the vertical direction, velocity is 0 at maximum height and
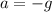 , so that
, so that
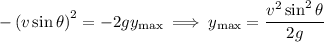
The projectile hits the ground when
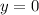 , which happens for
, which happens for
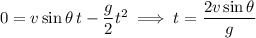
where we omit
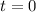 because we know the projectile starts on the ground. This means the maximum horizontal range is
because we know the projectile starts on the ground. This means the maximum horizontal range is
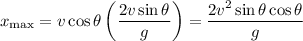
We're given that
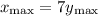 , so
, so
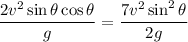
Solve for
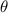 :
:
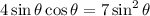

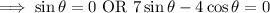
The first case suggests that
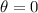 , but then both the maximum height and range would be 0, which would technically satisfy the given condition, but it's not an interesting solution.
, but then both the maximum height and range would be 0, which would technically satisfy the given condition, but it's not an interesting solution.
In the second case, we get
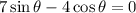
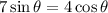
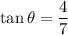
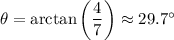
So the projectile was launched at an angle of about 29.7º.