Question

A projectile is fired in such a way that its horizontal range is equal to 7 times its maximum height. What is the angle of projection?

Answer 1

The projectile is fired with speed
`v` at an angle
`\theta` relative to the horizontal, so that the horizontal components of the initial velocity vector are

`v_x=v\cos\theta`

`v_y=v\sin\theta`

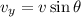
Its position vector has components

`x=v\cos\theta\,t`

`y=v\sin\theta\,t-\frac g2t^2`

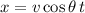
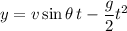
where
`g=9.80(\rm m)/(\mathrm s^2)`

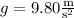
Recall that

`{v_f}^2-{v_i}^2=2a\Delta x`

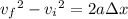
where
`v_i` and
`v_f` are the projectile's initial and final velocities,
`a` is its acceleration, and
`\Delta x` is its displacement.

In the vertical direction, velocity is 0 at maximum height and
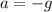`a=-g`, so that

`-\left(v\sin\theta\right)^2=-2gy_(\rm max)\implies y_(\rm max)=(v^2\sin^2\theta)/(2g)`

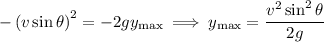
The projectile hits the ground when
`y=0`, which happens for

`0=v\sin\theta\,t-\frac g2t^2\implies t=\frac{2v\sin\theta}g`

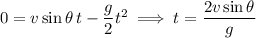
where we omit
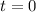`t=0` because we know the projectile starts on the ground. This means the maximum horizontal range is

`x_(\rm max)=v\cos\theta\left(\frac{2v\sin\theta}g\right)=\frac{2v^2\sin\theta\cos\theta}g`

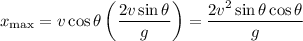
We're given that
`x_(\rm max)=7y_(\rm max)`, so

`\frac{2v^2\sin\theta\cos\theta}g=(7v^2\sin^2\theta)/(2g)`

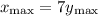Solve for
`\theta`:

`4\sin\theta\cos\theta=7\sin^2\theta`

`\sin\theta(7\sin\theta-4\cos\theta)=0`

`\implies\sin\theta=0\text{ OR }7\sin\theta-4\cos\theta=0`

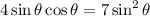
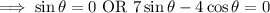
The first case suggests that
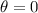`\theta=0`, but then both the maximum height and range would be 0, which would technically satisfy the given condition, but it's not an interesting solution.

In the second case, we get

`7\sin\theta-4\cos\theta=0`

`7\sin\theta=4\cos\theta`

`\tan\theta=\frac47`

`\theta=\arctan\left(\frac47\right)\approx29.7^\circ`

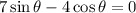
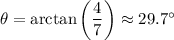
So the projectile was launched at an angle of about 29.7º.