Question

Find the minimum value of f (x, y) = (x -1)^2 + ( y - 4)^2 + (3- x - 2y)^2.

Answer 1

Find the critical points of f(x, y) :

`(\partial f)/(\partial x)=2(x-1)-2(3-x-2y)=4x+4y-8=0`

`(\partial f)/(\partial y)=2(y-4)-4(3-x-2y)=4x+10y-20=0`

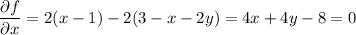
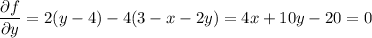
Subtract the first equation from the second to eliminate x and solve for y :

`(4x+10y-20)-(4x+4y-8)=0\implies 6y=12\implies y=2`

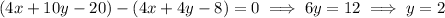
Solve for x :

`4x+4\cdot2-8=0\implies 4x=0\implies x=0`

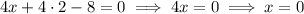
So f(x, y) has one critical point at (0, 2).

Compute the Hessian determinant of f(x, y) at this point:

`\mathbf H(x,y)=\begin{bmatrix}(\partial^2f)/(\partial x^2)&(\partial^2f)/(\partial x\partial y)\\(\partial^2f)/(\partial y\partial x)&(\partial^2f)/(\partial y^2)\end{bmatrix}=\begin{bmatrix}4&4\\4&10\end{bmatrix}`

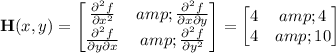
The Hessian has determinant 24 > 0, which indicates a minimum, so the minimum value of f(x, y) is f(0, 2) = 6.