Find the critical points of f(x, y) :
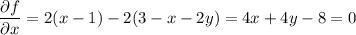
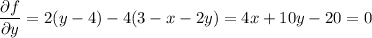
Subtract the first equation from the second to eliminate x and solve for y :
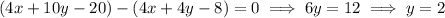
Solve for x :
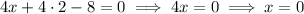
So f(x, y) has one critical point at (0, 2).
Compute the Hessian determinant of f(x, y) at this point:
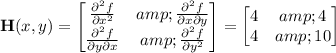
The Hessian has determinant 24 > 0, which indicates a minimum, so the minimum value of f(x, y) is f(0, 2) = 6.