Answer:
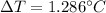
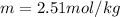
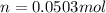
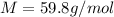
Step-by-step explanation:
Hello,
In case, for the boiling point raise we can write:
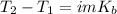
Whereas T2 accounts for the boiling point of the solution which is 101.286 °C, T1 the volume of pure water which is 100.000 °C, i the van't Hoff factor that for this problem is 1 due to the solute's non-volatility, m the molality of the solute and Kb the boiling point constant that is 0.512 °C/m. In such a way, the change in the temperature is:
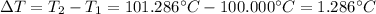
The molality is computed from the boiling point raise:
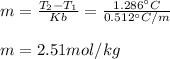
The moles are computed by multiplying the molality by the kilograms of water as the solvent (0.02002g):
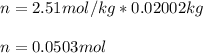
And the molecular mass by dividing the mass of the solute by its moles:
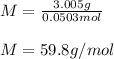
Best regards.