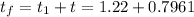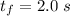Complete Question
The complete question is shown on the first uploaded image
Answer:
The time taken is
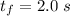
Step-by-step explanation:
Generally velocity of the noise in water is mathematically represented as

substituting into the variable with value given in the question

=>
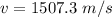
Generally the time taken is mathematically represented as
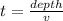
substituting into the variable with value given in the question
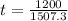
=>
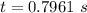
The velocity of the noise in air is mathematically represented as

Here R is the gas constant with value
![[R=286.6 m^2 /(sec^2 K) ][\tex]</p><p>So </p><p> [tex]v_w = √( 1.4 * 270 * 286.6)](https://img.qammunity.org/2021/formulas/physics/college/o8h51tvhq5r1dvoapnnwzxke1b5hfoyze1.png)

The time taken is
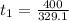
=>
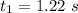
=> The total time is mathematially represented as