Answer:
*
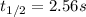
*
![[I_2]=0.011M](https://img.qammunity.org/2021/formulas/chemistry/college/73vwk7b0e2bu03rvrrb3zlwrc8qkzja6ds.png)
Step-by-step explanation:
Hello,
In this case, considering the reaction:
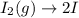
Which is first-order with respect to I₂, we can compute the half-life by:

Moreover, since the integrated rate law is:
![[I_2]=[I_2]_0exp(-kt)](https://img.qammunity.org/2021/formulas/chemistry/college/x27txsrhdxrz3htifu22bl2rjtuvj09ehx.png)
We can compute the concentration of iodine once 5.37 s have passed:
![[I_2]=0.048Mexp(-0.271s^(-1)*5.37s)\\\\](https://img.qammunity.org/2021/formulas/chemistry/college/u2ay6r1qq7y23z1bfynbgxoxylxqbr83gz.png)
![[I_2]=0.011M](https://img.qammunity.org/2021/formulas/chemistry/college/73vwk7b0e2bu03rvrrb3zlwrc8qkzja6ds.png)
Best regards.