Question

find the minimum diameter of steel which is used to raise a load of 4000n if the rod is not to exceed 95 mn/m^2

Answer 1

The minimum diameter of steel is 7.32 mm

Step-by-step explanation:

Given;

load raised by the steel, F = 4000 N

steel rating (tensile stress), σ = 95 MN/m² = 95 N/mm²

Area of the steel is given by;

`A = (F)/(\sigma) \\\\\pi r^(2) = (F)/(\sigma) \\\\r^(2) = (F)/(\pi \sigma) \\\\r = \sqrt{(F)/(\pi \sigma)} \\\\r = \sqrt{(4000)/(\pi (95))}\\\\r = 3.66 \ mm`

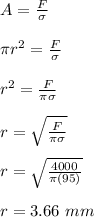
Thus, the minimum diameter of the steel = 2r

D = 2(3.66 mm)

D = 7.32 mm

Therefore, the minimum diameter of steel is 7.32 mm