Answer:
Kennan will be from home approximately an hour and 48 minutes.
Explanation:
We must know that total time (
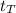 ) that Keenan will be from home is the sum of run (
) that Keenan will be from home is the sum of run (
 ), hang out (
), hang out (
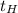 ) and walk times (
) and walk times (
 ), measured in hours:
), measured in hours:

If Keenan runs and walks at constant speed, then equation above can be expanded:
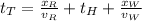
Where:
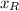 ,
,
 - Run and walk distances, measured in miles.
- Run and walk distances, measured in miles.
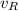 ,
,
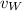 - Run and walk speeds, measured in miles per hour.
- Run and walk speeds, measured in miles per hour.
Given that
 ,
,
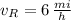 ,
,
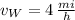 and
and
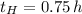 , the total time is:
, the total time is:
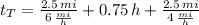
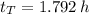 (
(
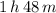 )
)
Kennan will be from home approximately an hour and 48 minutes.