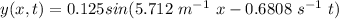Answer:
The simple harmonic wave function is
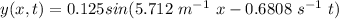
Step-by-step explanation:
Generally a sine wave is mathematically represented as
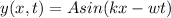
Here A is the amplitude which is mathematically represented as

substituting 0.25 m for Z we have that

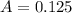
k is the wave number which is mathematically represented as
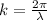
substituting 1.1 m for (wavelength ) we have
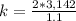
=>
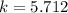
w is the angular frequency which is mathematically represented as
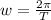
Here T is the period which is mathematically represented as
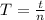
substituting 13 wave pass for n and
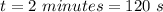 for t
for t
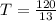

So
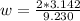
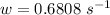
So