Question

Solve by using the quadratic formula:
x² - 6x + 7-O

Answer 1

Explanation:

Hey there!!

The equation is;

`{x}^(2) - 6x + 7 = 0`

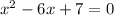
Now, Comparing it with ax^2 + bx + c = 0. we get;

a = 1, b= -6 and c = 7

Use quadratic formula.

`x = \frac{ - b + - \sqrt{ {b}^(2) - 4ac} }{2a}`

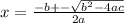
Put all values.

`x = \frac{ + 6 + - \sqrt{( { - 6)}^(2) - 4 * 1 * 7} }{2 * 1}`

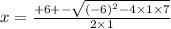
Simplify them.

`x = (6 + - √(36 - 28) )/(2)`

`x = ( 6 + - √(8) )/(2)`

`x = (6 + - 2 √(2) )/(2)`

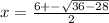
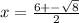
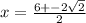
Taking positive (+).

`x = (6 + 2 √(2) )/(2)`

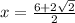
Simplifying them.

`x = (2(3 + √(2) ))/(2)`

`x = 3 + √(2)`

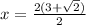
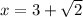
Now, Taking negative (-).

`x = (6 - 2 √(2) )/(2)`

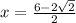
Simplifying them.

`x = (2(3 - √(2) ))/(2)`

`x = 3 - √(2)`

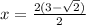
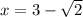
Therefore the answer is;

`x = 3 + √(2) \: and \: 3 - √(2)`

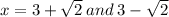
Hope it helps...

Answer 2

it is x=7

x=-1

Explanation:

i using the quadratic formula