Explanation:
Hey there!!
The equation is;

Now, Comparing it with ax^2 + bx + c = 0. we get;
a = 1, b= -6 and c = 7
Use quadratic formula.
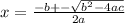
Put all values.
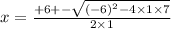
Simplify them.
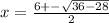

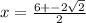
Taking positive (+).
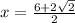
Simplifying them.
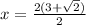
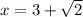
Now, Taking negative (-).
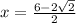
Simplifying them.


Therefore the answer is;
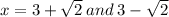
Hope it helps...