Explanation:
Let
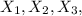 . . . ,Xn be the random sample of n employee's sick days. It is given that the random samples follows the Normal distribution along with standard deviation of 7 days. Let
. . . ,Xn be the random sample of n employee's sick days. It is given that the random samples follows the Normal distribution along with standard deviation of 7 days. Let


or
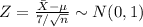
So,
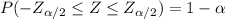
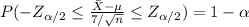
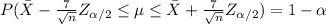
Therefore, the confidence interval of the population mean for α = 0.05 is
=
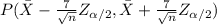
=
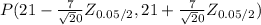
= (17.93, 24.07)