Answer:
a
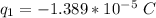 ,
,
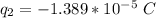
OR
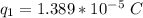 ,
,

b
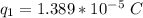 and
and

Step-by-step explanation:
Generally the force exerted on the string is mathematically represented as
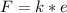
substituting values 180 N/m for k and 0.024 m for e
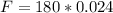
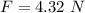
This force can also equivalent to the electrostatic force between the charges i.e
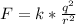
substituting
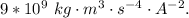 for k and ( 0.34 + 0.024 = 0.364 m) for r we have
for k and ( 0.34 + 0.024 = 0.364 m) for r we have
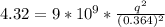
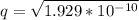
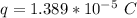
Given the spring was stretched it means that the force between the charges is a repulsive for which tell us that both charge are of the same sign thus the possible algebraic signs of the charges are
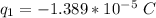 ,
,
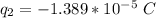
OR
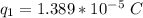 ,
,
