Question

Two wooden members of uniform rectangular cross section are joined using a simple glued scarf splice. The maximum allowable shearing stress and maximum allowable normal stress in the glued splice is 50 MPa and 100 MPa, respectively. The cross-section area of the glued member is 400 mm2. (a) What should the value of the angle  be to achieve maximum load Fmax? (b) What is the magnitude of the maximum load Fmax?

Answer 1

a). α = 26.57

b). Maximum load is 50 .kN

Step-by-step explanation:

a).

The normal force is given by

N = σ A cosec β

where, σ is the normal stress

A is the cross sectional area

Similarly, shear force is given by

S= τ A cosec β

where, τ is the shearing stress

Now from the figure,

tan β = S/N

= τ/σ

Therefore,
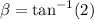`$\beta = \tan^(-1)(2)$` = 63.43

α = 90 - β = 26.57

b).

The normal force is given by

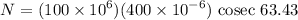
`$N=(100* 10^6)(400* 10^(-6)) \text{ cosec}\ 63.43$`

`$N=44.78* 10^3$` N

We have

`$\Sigma F_y=0$`

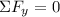
∴ N - F sin β = 0

⇒ F = N / sin β

=
`$(44.72* 10^3)/(\sin(63.43)) = 50* 10^3 N$`

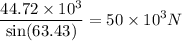
Similarly,

The shear force is given by

S = τ A cosec β

=
`$(50* 10^6)(400* 10^(-6)) \text{ cosec}\ 63.43 = 22.36* 10^3 N$`

`$\Sigma F_x=0$`

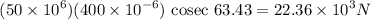
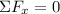
∴ S - F cos β = 0

⇒ F = S / cos β

`$(22.36* 10^3)/(\cos(63.43)) = 49.99* 10^3 N$`

Therefore, force is 50 kN.