Question

A freight and passenger train share the same track. The average speed of the freight train is 45 mph, whereas that of the passenger train is 70 mph. The passenger train is scheduled to leave 20 minutes after the freight train departs from the same station. Determine the location where a siding would need to be provided to allow the passenger train to pass the freight train. Also determine the time it takes for the freight train to arrive at the siding. As a safety precaution, the separation headway between the two trains at the siding should be at least equal to 6 minutes.

Answer 1

The first siding should be located at 30 miles

The time for the freight to arrive at the siding is 40 minutes

Explanation:

From the given information:

Let
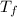`T_f` represent the time for the freight train

Also, let
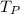`T_P` represent the time at which the passenger train reach the location

Let Y represents the location where the location of the siding of the track needed to take place.

Thus, for freight time:

`T_f = (Y)/(45) --- (1)`

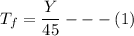
The siding location is:

`T_P = (2)/(6)+(Y)/(70)`

`T_P =0.333+(Y)/(70) --- (2)`

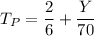
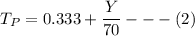
To determine Y:

`T_P -T_f = 0.1 --- (3)`

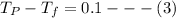
replacing the value of
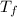`T_f` and
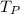`T_P` in the above equation (3), we have:

`0.333+(Y)/(70) - (Y)/(45) =0.1`

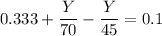
collecting like terms, we have:

`(Y)/(70) - (Y)/(45) =0.1-0.333`

`(45Y- 70Y)/(3150) =-0.233`

`(-25Y)/(3150) =-0.233`

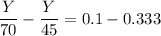
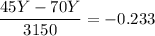
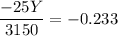
- 25Y = -0.233 × 3150

- 25Y = -733.95

Y = -733.95/-25

Y = 29.36 miles

Y
`\simeq` 30 miles to the nearest whole number

Thus, the first siding should be located at 30 miles

To estimate the time for the fight to arrive the siding, we replace 30 miles for
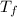`T_f` in equation (1).

Then, we have:

`T_f = (Y)/(45)`

`T_f = (30)/(45)`

`T_f =0.667\ hr`

`T_f =(0.667 * 60 )minutes`

`T_f =40.2 \ minutes`

`\mathsf{T_f \simeq 40 \ minutes}`

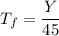
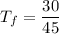
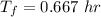
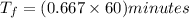
Thus, the time for the freight to arrive at the siding is 40 minutes