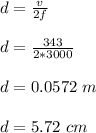Question

The overall length of a piccolo is 30.0 cm. The resonating air column is open at both ends. (a) Find the frequency of the lowest note a piccolo can sound. (Assume that the speed of sound in air is 343 m/s.) Hz (b) Opening holes in the side of a piccolo effectively shortens the length of the resonant column. Assume the highest note a piccolo can sound is 3 000 Hz. Find the distance between adjacent antinodes for this mode of vibration.

Answer 1

(a) the frequency of the lowest note the piccolo can sound is 571.7 Hz

(b) the distance between adjacent antinodes is 5.72 cm

Step-by-step explanation:

(a)

Given;

length of piccolo, L = 30 cm = 0.3 m

the speed of sound in air is 343 m/s

The wavelength of a pipe open at both ends, for the first harmonic is given;

L = A → N + N → A

L = λ / 4 + λ / 4

L = λ / 2

λ = 2L

λ = 2 x 0.3 = 0.6 m

The fundamental frequency (lowest frequency) is given by;

f₀ = v / λ

f₀ = (343 / 0.6)

f₀ = 571.7 Hz

(b)

Given;

highest note, f = 3000 Hz

the distance between adjacent antinodes is given by;

`d = (v)/(2f)\\\\ d = (343)/(2*3000)\\\\ d = 0.0572 \ m\\\\d = 5.72 \ cm`