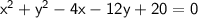Question

This circle is centered at the point (2,6), and the length of its radius is 4. What is the equation of the circle?

Answer 1

The equation of the circle with centre (h,k) and radius (r) can be written as :-

`\\ \qquad \sf \: {(x - h)}^(2) + {(y - k)}^(2) = {r}^(2) \\`

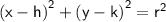
So, we are given with :-

• h = 2
• k = 6
• r = 4

Now, by putting their value we can write the equation as :-

`\\ \qquad\sf \: {(x - 2)}^(2) - {(y - 6)}^(2) = {4}^(2) (16) \\`

Expanding this, we get :-

`\\ \sf {x}^(2) - 4x + 4 + { y}^(2) - 12y + 36 = 16 \\`

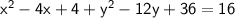
Rearranging and by subtracting by 16 from both sides we got standard polynomial as -

`\\ \sf \: {x}^(2) + {y}^(2) - 4x - 12y + 20 = 0 \\`