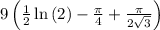Answer:
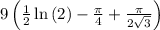
Explanation:
We are given the integral 9 arctan(1/x)dx on the interval x[ from 1 to √3 ].
Now let's say that u = arctan(1/x). The value of 'du' would be as follows:
du = - x / (1 + x²) * dx
If we apply integration by parts, v = 1, and of course u = arctan(1/x):
=> 9x arctan(1/x) − ∫ -9x dx / (x² + 1)
=> 9[x arctan(1/x) - ∫ - x / (1 + x²) * dx] on the interval x[ from 1 to √3 ]
Let's now simplify the expression ' ∫ - x / (1 + x²) * dx':
=> (Take the constant out, in this case constant = - 1), - ∫ x / (1 + x²) * dx
=> (Apply u-substitution, where u = 1 + x²), - ∫ 1/2u * du
=> (Take constant out again, in this case 1/2), - 1/2 ∫ 1/u * du
=> (Remember that 1/u * du = In( |u| )), - 1/2In( |u| )
=> (Substitute back 'u = 1 + x²), - 1/2In| 1 + x² |
So now we have the expression '9[x arctan(1/x) + 1/2In| 1 + x² |]' on the interval x[ from 1 to √3 ]. Let's further simplify this expression;
![9\left[x\arctan \left((1)/(x)\right)+(1)/(2)\ln \left|1+x^2\right|\right]^(√(3))_1\\\\=> 9\left[(1)/(2)\left(2x\arctan \left((1)/(x)\right)+\ln \left|1+x^2\right|\right)\right]^(√(3))_1](https://img.qammunity.org/2021/formulas/mathematics/college/my1hf7xzltkpwukj42iwb2bc2243jcx3ms.png)
Now computing the boundaries we have the following answer: