Let as consider the complete ques is : Ray QS bisects ∠PQR. Solve for x and find m∠PQR. m∠PQS = 3x ; m∠SQR = 5x-20.
Given:
Ray QS bisects ∠PQR.
m∠PQS = 3x
m∠SQR = 5x-20
To find:
The value of x and m∠PQR
Solution:
Ray QS bisects ∠PQR. So,
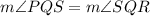
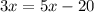
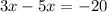
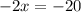
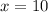
The value of x is 10.
Now,
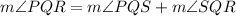
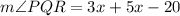
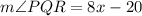
Put x=10,
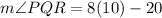
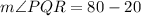
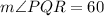
Therefore, the m∠PQR is 60 degrees.