Answer:
(2)
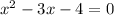
Explanation:
Standard form of a quadratic equation:

When factoring a quadratic (finding the roots) we find two numbers that multiply to
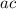 and sum to
and sum to
 , then rewrite
, then rewrite
 as the sum of these two numbers.
as the sum of these two numbers.
So if the roots sum to 3 and multiply to -4, then the two numbers would be 4 and -1.
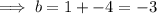
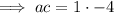
As there the leading coefficient is 1,
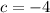 .
.
Therefore, the equation would be:
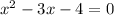
Proof
Factor
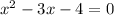
Find two numbers that multiply to
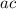 and sum to
and sum to
 .
.
The two numbers that multiply to -4 and sum to -3 are: -4 and 1.
Rewrite
 as the sum of these two numbers:
as the sum of these two numbers:
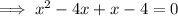
Factorize the first two terms and the last two terms separately:
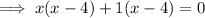
Factor out the common term
 :
:

Therefore, the roots are:
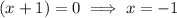
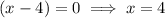
So the sum of the roots is: -1 + 4 = 3
And the product of the roots is: -1 × 4 = -4
Thereby proving that
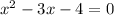 has roots whose sum is 3 and whose product is -4.
has roots whose sum is 3 and whose product is -4.