Question

What is the equation of a sine function with an amplitude of 2 and a period of 4

Answer 1

Answer: C

Explanation:

For this problem, we need to know the standard form of a sine function and the meaning of each part.

Standard form:
`y=asin[b(x-h)]+k`

a=amplitude

b=period

h=phase shift

k=vertical replacement/shifting

Now that we know the standard form and the components, we know that we can forget about k and plug in 0 for h. This would leave us with
`y=asin[b(x)]`. We know that the amplitude is 2, therefore, a=2. To find the period, you divide 2π by the given period.
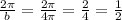`(2\pi )/(b) =(2\pi )/(4\pi ) =(2)/(4) =(1)/(2)`, therefore, b=1/2.

`y=asin[b(x)]` [plug in a=2]

`y=2sin[b(x)]` [plug in b=1/2]

`y=2sin((1)/(2)x)`

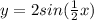
Therefore, C is the correct answer.