By Bernoulli's Principle :
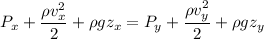
Since , pipe is horizontal so every point is at same height .
So ,
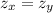 .
.
The equation will reduced to :
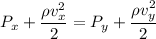 ..... 1 )
..... 1 )
Also flow rate will be constant :
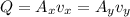
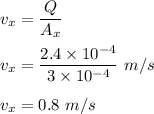

Now ,
![P_x-P_y=(\rho v_y^2)/(2)-(\rho v_x^2)/(2)\\\\P_x-P_y=\rho[( v_y^2)/(2)-(v_x^2)/(2)]\\\\P_x-P_y=1000* [( 4^2)/(2)-(0.8^2)/(2)]\\\\P_x-P_y=7680\ Pa](https://img.qammunity.org/2021/formulas/physics/high-school/tqxsxqyxca71870v5czdnwd5jgsvtyi3fv.png)
Difference in pressure between X and Y is most near to 7700 Pa.
Hence, this is the required solution.