Question

Use the number line​ below, where ​, ​, and . a. What is the value of​ y? b. Find RS and ST. R S T a. What is the value of​ y? y 4 ​(Type an integer or a​ decimal.) b. Find RS and ST. RS 4.2 ​(Type an integer or a​ decimal.)

Answer 1

Guy above me is Wrong its 14

Explanation:

Answer 2

y = 4

RS = 35

ST = 26

Explanation:

Given:

RS = 8y + 3

ST = 5y + 6

RT = 61

Required:

a. Value of y

b. Numerical lenght of RS and ST

SOLUTION:

a. Points R, S and T are collinear, therefore, based on segment addition postulate, the following equation can be created to find the value of y:

`RS + ST = RT`

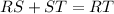
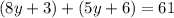`(8y + 3) + (5y + 6) = 61` (substitution)

Solve for y

`8y + 3 + 5y + 6 = 61`

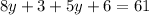
Combine like terms

`8y + 5y + 3 + 6 = 61`

`13y + 9 = 61`

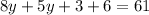
Subtract 9 from both sides

`13y + 9 - 9 = 61 - 9`

`13y = 52`

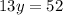
Divide both sides by 13

`(13y)/(13) = (52)/(13)`

`y = 4`

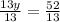
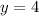
b. RS = 8y + 3

Plug in the value of y

RS = 8(4) + 3 = 32 + 3

RS = 35

ST = 5y + 6

Plug in the value of y

ST = 5(4) + 6 = 20 + 6

ST = 26