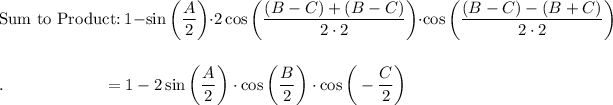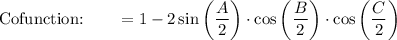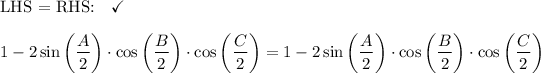Answer: see proof below
Explanation:
Given: A + B + C = π → A = π - (B + C)
→ B + C = π - A
Use the Pythagorean Identity: cos² A + sin² A = 1 → sin² A = 1 - cos² A
Use Double Angle Identities: cos 2A = 2 cos² A - 1 → cos² A = (cos 2A + 1)/2
→ cos A = 1 - 2 sin² (A/2)
Use Sum to Product Identity: cos A + cos B = 2 cos [(A + B)/2] · cos [(A - B)/2]
Use Cofunction Identities: cos (π/2 - A) = sin (A)
sin (π/2 - A) = cos A
cos (-A) = cos (A)
Proof LHS → RHS:
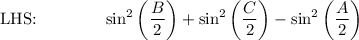
![\text{Pythagorean:}\qquad 1-\cos^2 \bigg((B)/(2)\bigg)+1-\cos^2 \bigg((C)/(2)\bigg)-\bigg[1-\cos^2 \bigg((A)/(2)\bigg)\bigg]\\\\\\.\qquad \qquad \qquad =1-\cos^2 \bigg((B)/(2)\bigg)-\cos^2 \bigg((C)/(2)\bigg)+\cos^2 \bigg((A)/(2)\bigg)](https://img.qammunity.org/2021/formulas/mathematics/high-school/586rkmv5ehgcfnrm4oh9311ico2ql2qgri.png)
![\text{Double Angle:}\quad 1-\bigg((\cos(2\cdot (B)/(2))+1)/(2)\bigg)-\bigg((\cos (2\cdot (C)/(2))+1)/(2)\bigg)+\bigg((\cos (2\cdot (A)/(2))+1)/(2)\bigg)\\\\\\.\qquad \qquad \qquad =1-(\cos B)/(2)-(1)/(2)-(\cos C)/(2)-(1)/(2)+(\cos A)/(2)+(1)/(2)\\\\\\.\qquad \qquad \qquad =(1)/(2)[1-(\cos B+\cos C)+\cos A]](https://img.qammunity.org/2021/formulas/mathematics/high-school/2op3x6n2gbqqunhlfwtvmv8ce37i2itsb8.png)
![\text{Sum to Product:}\qquad (1)/(2)\bigg(1-\bigg[2\cos \bigg((B+C)/(2)\bigg)\cdot \cos \bigg((B-C)/(2)\bigg)\bigg]+\cos A\bigg)](https://img.qammunity.org/2021/formulas/mathematics/high-school/bc5zycwgdc2bgpymjwzf17rtm3vn4ek2d8.png)
![\text{Given:}\qquad (1)/(2)\bigg(1-\bigg[2\cos \bigg((\pi -A)/(2)\bigg)\cdot \cos \bigg((B-C)/(2)\bigg)\bigg]+\cos A\bigg)](https://img.qammunity.org/2021/formulas/mathematics/high-school/pujdyf018fjxqgzp91ma5sdqs8j6y5wict.png)
![\text{Cofunction:}\qquad (1)/(2)\bigg(1-\bigg[2\sin \bigg((A)/(2)\bigg)\cdot \cos \bigg((B-C)/(2)\bigg)\bigg]+\cos A\bigg)](https://img.qammunity.org/2021/formulas/mathematics/high-school/cxypurzanezqwx1jmmmib54yd6clw8217m.png)
![\text{Double Angle:}\qquad (1)/(2)\bigg[1-2\sin \bigg((A)/(2)\bigg)\cdot \cos \bigg((B-C)/(2)\bigg)+1-2\sin^2 \bigg((A)/(2)\bigg)\bigg]\\\\\\.\qquad \qquad \qquad =(1)/(2)\bigg[2-2\sin \bigg((A)/(2)\bigg)\cdot \cos \bigg((B-C)/(2)\bigg)-2\sin^2 \bigg((A)/(2)\bigg)\bigg]\\\\\\.\qquad \qquad \qquad =1-\sin \bigg((A)/(2)\bigg)\cdot \cos \bigg((B-C)/(2)\bigg)-\sin^2 \bigg((A)/(2)\bigg)](https://img.qammunity.org/2021/formulas/mathematics/high-school/bc40ynwnov2aasfxj8zf565s0qeb9ehwm8.png)
![\text{Factor:}\qquad \qquad 1-\sin \bigg((A)/(2)\bigg)\bigg[ \cos \bigg((B-C)/(2)\bigg)-\sin \bigg((A)/(2)\bigg)\bigg]](https://img.qammunity.org/2021/formulas/mathematics/high-school/fpkqnidl7jeh5v9sbezflts6gwrzm1msww.png)
![\text{Given:}\qquad \qquad 1-\sin \bigg((A)/(2)\bigg)\bigg[ \cos \bigg((B-C)/(2)\bigg)-\sin \bigg((\pi -(B+C))/(2)\bigg)\bigg]](https://img.qammunity.org/2021/formulas/mathematics/high-school/86l79r6m7cpuauscryscqi45upk38cy963.png)
![\text{Cofunction:}\qquad 1-\sin \bigg((A)/(2)\bigg)\bigg[ \cos \bigg((B-C)/(2)\bigg)+\cos \bigg((B+C)/(2)\bigg)\bigg]](https://img.qammunity.org/2021/formulas/mathematics/high-school/n45grhq3s5erg7da2rhse03h7zbrmmg114.png)