Answer:
Q7) ( 2,-2)
Q8) (- 0.5 , -2)
Explanation:
As we have to find the mid-points of the line segments, the line segments will be divided in same ratio i.e. 1:1 (∵ A Mid-point divides a line segment into equal parts )
According to Section formula ,

where (m,n) are the ratios in which a line segment is divided & ( x¹ , y¹ ) ( x², y²) are the co-ordinates of a line segment.
In Q7 ,
x¹ = 3 , y¹ = -9 , x² = 1 , y² = 5 & m = n = 1
So putting the section formula here gives :-
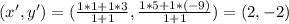
In Q8 ,
x¹ = 5 , y¹ = -1 , x² = -6 , y² = -3
So putting the section formula here gives :-
