Question

Rural and urban students are equally

likely to get admission in a college. If 100
students get admission, then the probability
that more rural students get admission than
urban students is

Answer 1

The answer is below

Explanation:

Using binomial probability:

p = probability of a rural student getting admission = 1/2

q = probability of a rural student not getting admission = 1/2

n = number of students = 100

P(x) =
`C(n,x) p^xq^{(n-x)`

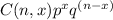
But
`p^xq^(n-x)=(1)/(2)^x(1)/(2)^(n-x)=(1)/(2)^(n)`

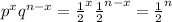
P(x > 50) = P(x = 51) + P(x = 52) + P(x = 53) + . . . + P(x = 100)

P(x > 50) =
`(1)/(2) ^(100)[C(100,51)+C(100,52)+C(100,53)+\ .\ .\ .+C(100,100)]\\`

`P(x>50)=(1)/(2)^(100) ((1)/(2)( 2^(100)-C(100,50)))\\\\P(x>50)=((1)/(2)^(100) *(1)/(2)*2^(100))- ((1)/(2)^(100) *(1)/(2)*C(100,50))\\\\P(x>50)=(1)/(2)[(2^(-100)*2^(100))-((1)/(2)^(100) *C(100,50))]\\ \\P(x>50)=(1)/(2)[1-(1)/(2)^(100) *C(100,50)]`