Question

What are the solutions of the equation x4 – 5x2 – 36 = 0? Use factoring to solve. x = ±2 and x = ±3 x = ±2i and x = ±3 x = ±2 and x = ±3i x = ±2i and x = ±3i

Answer 1

B). x = ±2i and x = ±3

Explanation:

Answer 2

`x=\pm 3\text{ or } x=\pm 2i`

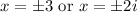
Explanation:

So we have the equation:

`x^4-5x^2-36=0`

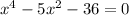
Let's let u equal x² so:

`u^2-5u-36=0`

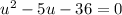
Factor. We can use -9 and 4. So:

`u^2+4u-9u-36=0`

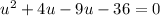
From the first two terms, factor out a u.

From the last two terms, factor out a -9. So:

`u(u+4)-9(u+4)=0`

Grouping:

`(u-9)(u+4)=0`

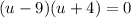
Zero Product Property:

`u-9=0 \text{ or } u+4=0`

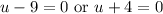
On the left, add 9. On the right, subtract 4:

`u=9\text{ or } u=-4`

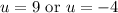
Substitute back u:

`x^2=9\text{ or } x^2=-4`

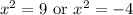
Take the square root:

`x=\pm 3\text{ or } x=\pm 2i`

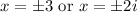
And we're done!

Our answer is the Second option.