Question

(Number 5)help plzzz

Answer 1

See below.

Explanation:

So we want to prove that:

`\sqrt8+\sqrt2=3\cdot 2^{(1)/(2)}`

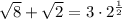
First, simplify √8. This is the same as:

`\sqrt8=√(4\cdot 2)=\sqrt4\cdot\sqrt2=2\sqrt2`

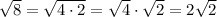
Therefore, our equation is now:

`2\sqrt2+\sqrt2=3\cdot2^{(1)/(2)}`

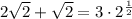
Combine like terms on the left:

`3\sqrt2=3\cdot 2^(1)/(2)}`

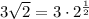
The square root of something is the same as taking that number to the one-half power. Thus:

`3(2)^(1)/(2)}=3\cdot 2^(1)/(2)}`

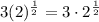
Rewrite:

`3\cdot2^(1)/(2)}\stackrel{\checkmark}{=}3\cdot2^(1)/(2)}`

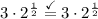
And we're done!