Answer:
See below.
Explanation:
So we want to prove that:
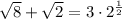
First, simplify √8. This is the same as:
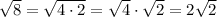
Therefore, our equation is now:
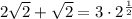
Combine like terms on the left:
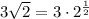
The square root of something is the same as taking that number to the one-half power. Thus:
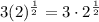
Rewrite:
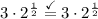
And we're done!