Answer:

==============================================
Work Shown:
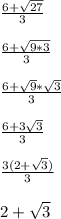
The idea with simplifying the square root (steps 2 through 4) has us factoring 27 so that one factor is a perfect square. We want the largest perfect square factor possible.
That way when we use the rule sqrt(x*y) = sqrt(x)*sqrt(y), we pull out that perfect square to then use the rule sqrt(x^2) = x where x is nonnegative.
After simplifying the square root, we factor out the GCF and then cancel out the 3's.