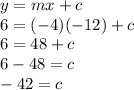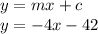Answer:
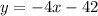
Explanation:
The equation of the line that is parallel to the line we are trying to find is
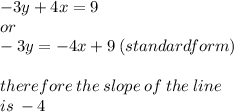
We can recall that when two lines are parallel it means that they have the same slope. Therefore the slope of the line we are trying to find is also -4. We now know that:
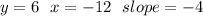
Therefore the equation of the line is: