Answer:

Explanation:
We are given the indefinite integral:
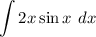
Using by-part method, we have to substitute u-term and dv appropriately.
By-part is an integration of product rules, when integrated the product rules of differentiation, we’ll obtain:
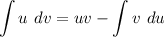
Above is by-part method/formula.
Where 4 terms are presented:
Our main terms to substitute are u and dv which mean u-term has to be a function that’s differentiatable and dv has to be a function that’s integratable.
The main concept of by-part is to understand how to substitute appropriately which you can simply follow below:
LIATE
Stands for Logarithm, Inverse (Trigonometry), Algebraic, Trigonometric and Exponential.
These are in orders from first to last on what to let u-term first. That means logarithm functions must be the first to substitute themselves as u-term, so if you encounter a logarithmic function and a polynomial function, you must let u = logarithmic function while dv = polynomial.
In this case, we have 2x which is polynomial and sin(x) which is trigonometric. According to LIATE, we have to let Algebraic or Polynomial 2x be first to substitute as u-term, that means our dv is trigonometric sin(x).
Therefore, we have:
- u = 2x
- du = 2dx
- dv = sin(x)dx
- v = -cos(x)
Now, substitute these terms in accordingly to formula of by-part.
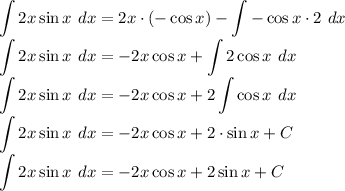
__________________________________________________
Summary
Property
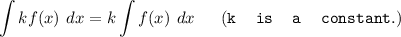
Only shown in explanation.
By-Part
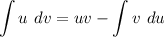
LIATE
The functions in order that should be u-term from first to last.
- Logarithm
- Inverse Trigonometric
These functions above do not have integration formula by default.
- Polynomial (Algebraic)
- Trigonometric
- Exponential (Last since it’s the easiest to integrate, especially natural exponential)
Indefinite Integral
Make sure to always add + C after evaluating the integral, regardless what multiplies or attempts to affect + C, we must always add + C.
__________________________________________________