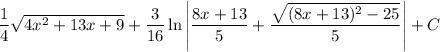Question

Integral of x+2/

`\sqrt{x { + 2x + 3}^(2) }`
​

Answer 1

Looks like the integral should be

`\displaystyle\int(x+2)/(√(x+(2x+3)^2))\,\mathrm dx`

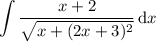
Expand the denominator:

`\displaystyle\int(x+2)/(√(4x^2+13x+9))\,\mathrm dx`

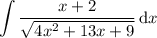
Notice that

`u=4x^2+13x+9\implies \mathrm du=(8x+13)\,\mathrm dx`

In order to use this substitution, expand the integral as

`\displaystyle\frac18\int(8x+13)/(√(4x^2+13x+9))\,\mathrm dx+\frac38\int(\mathrm dx)/(√(4x^2+13x+9))`

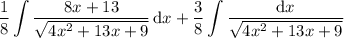
In the first integral, use the previously mentioned substitution:

`\displaystyle\frac18\int(8x+13)/(√(4x^2+13x+9))\,\mathrm dx=\frac18\int(\mathrm du)/(\sqrt u)=\frac14\sqrt u`

`=\frac14√(4x^2+13x+9)`

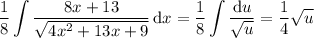
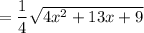
In the second integral, complete the square in the denominator:

`4x^2+13x+9=4\left(x+\frac{13}8\right)^2-(25)/(16)`

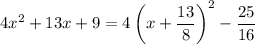
Now substitute

`x=\frac58\sec t-\frac{13}8\implies\mathrm dx=\frac58\sec t\tan t\,\mathrm dt`

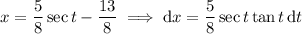
so that

`\sec t=\frac{8x+13}5`

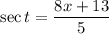
Then

`4x^2+13x+9=(25)/(16)(\sec^2t-1)=(25)/(16)\tan^2t`

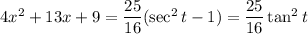
and the integral becomes

`\displaystyle((15)/(64))/(\frac54)\int(\sec t\tan t)/(√(\tan^2t))\,\mathrm dt=\frac3{16}\int\sec t\,\mathrm dt`

`=\frac3{16}\ln|\sec t+\tan t|`

`=\frac3{16}\ln\left|\frac{8x+13}5+\frac{√((8x+13)^2-25)}5\right|`

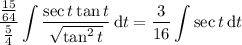
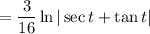
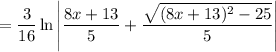
So, the integral is

`\frac14√(4x^2+13x+9)+\frac3{16}\ln\left|\frac{8x+13}5+\frac{√((8x+13)^2-25)}5\right|+C`