Question

Find mDCAˆ. the question says that the angle is 3x+19 the smaller arc is 91 and the bigger is 17x-3 it is one of those problems were the difference in the arcs divided by two equals the angle

Answer 1

Answer: Option C.

Explanation:

Let as consider the below figure is attached below.

We know that angle between tangent and secant is half of difference of major and minor arcs.

`\angle ABC=(arc(AD)-arc(AC))/(2)`

`3x+19=(17x-3-91)/(2)`

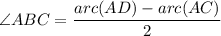
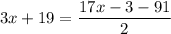
Multiply both sides by 2.

`6x+38=17x-94`

`38+94=17x-6x`

`132=11x`

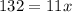
Divide both sides by 11.

`12=x`

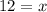
The value of x is 12.

`arc(AD)=17(12)-3`

`arc(AD)=204-3`

`arc(AD)=201^(\circ)`

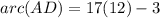
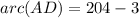
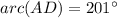
Now,

`arc(DCA)=360^\circ-arc(AD)`

`arc(DCA)=360^\circ-201^(\circ)`

`m\widehat {DCA}=159^(\circ)`

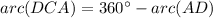
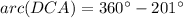
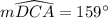
Therefore, the correct option is C .