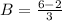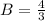Answer:

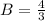
Explanation:
Given
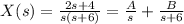
Required
Find A and B
The expression can be rewritten as
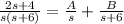
Take LCM of the right hand side
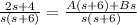
Cancel out the denominators
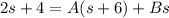
Open Bracket
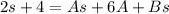
Reorder
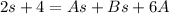
By direct comparison:
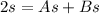
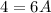
Solving
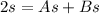
Divide through by s
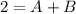
Solve for A in
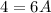

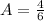

Substitute
 for A in
for A in
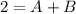
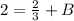
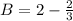
LCM