Question

Part A

Suppose that you want to construct a line with slope m=3 that passes through the point (2,1). You would begin by setting up the equation
y=3x+b.
If you plug in the coordinates for any point on that line, the two sides of the equation will be equal. Once you've done this, you can solve for b. What is the value of b?
Express your answer as an integer.
Part B
Suppose that you want to find the equation for a line that passes through the two points (0,3) and (4,9). What is the slope of this line?
Express your answer numerically.

Answer 1

a) b = -5

b) slope = 3/2

Step-by-step explanation:

a) The equation of a line is given as y = mx + b, where m is the slope of the line and b is the intercept on the y axis.

Given that y = 3x + b and it passes through the point (2, 1). Hence when x = 2, y = 1. Therefore, substituting for x and y:

1 = 3(2) + b

1 = 6 + b

b = 1 - 6

b = -5

b) The equation of a line passing through two points (
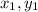`x_1,y_1`) and
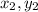`x_2,y_2` is given by:

`y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)`

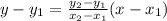
The equation of the line passing through the two points (0,3) and (4,9) is:

`y-3=(9-3)/(4-0)(x-0)\\ \\y-3=(3)/(2)x\\ \\y = (3)/(2)x+3`

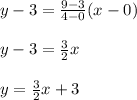
Comparing y = (3/2)x + 3 with y = mx + b, the slope (m) is 3/2