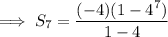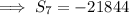Question

Find the sum of the geometric series given the following information

Answer 1

-21844

Explanation:

Finding n

• aₙ = arⁿ⁻¹

• -16384 = -4(4)ⁿ⁻¹
• 4ⁿ⁻¹ = 4096
• 4ⁿ⁻¹ = 64²
• 4ⁿ⁻¹ = (8²)²
• 4ⁿ⁻¹ = (4³)²
• n - 1 = 6
• n = 7

Finding The Sum

• S₇ = -4(4⁷ - 1) / 4 - 1
• S₇ = -4 (16383) / 3
• S₇ = -65536/3
• S₇ = -21844

Answer 2

-21844

Explanation:

Given:

• 
  `a_1=-4`
• 
  `a_n=-16384`
• 
  `r=4`

First find n by using the general form of a geometric sequence:
`a_n=ar^(n-1)` (where a is the first term and r is the common ratio)

`\implies -16384=(-4)(4)^(n-1)`

`\implies 4^(n-1)=(-16384)/(-4)`

`\implies 4^(n-1)=4096`

`\implies \ln 4^(n-1)=\ln 4096`

`\implies (n-1)\ln 4=\ln 4096`

`\implies n=(\ln 4096)/(\ln 4)+1`

`\implies n=6+1`

`\implies n=7`

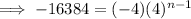
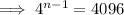
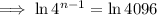
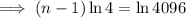
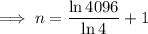
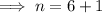
Sum of the first n terms of a geometric series:

`S_n=(a(1-r^n))/(1-r)`

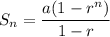
(where a is the first term and r is the common ratio)

Substituting the given values and the found value of n into the formula:

`\implies S_(7)=((-4)(1-4^7))/(1-4)`

`\implies S_(7)=-21844`