Question

PLEASE HELP!!! i’ve been stuck on this for so long!!!

Determine the number of terms in the geometric series 2+8+32+...+2048

Answer 1

6 terms

Explanation:

we have

`2+8+32+..+2048`

we need to identify a pattern so

from 2 to 8 what could have happened?

well you could have added 6 and get 8

so that means that to 8 you have to add 6 and get 32

WRONG

so adding is not an option

what else could have happened?

well you could have multiplied by 4 and get 8

so that means that to 8 you have to multiply by 4 and get 32

which is true

so the geometric series is

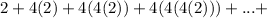`2+4(2)+4(4(2))+4(4(4(2)))+...+` what?

you can see that in the 2nd term we have 1 four, in the 3rd we have 2 fours

so we can conclude in the nth term we have n-1 fours

so the formula is

`2+8+32+...+4^(n-1) *2`

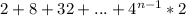
so we need to determine when

`4^(n-1)*2=2048`

`4^(n-1)*2*(1)/(2) =2048*(1)/(2) \\\\4^(n-1)=1024`

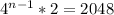
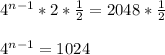
if we factorize 4 as
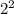`2^2` and 1024 as
`2^(10)`

we have

`(2^2)^(n-1)=2^(10)\\\\2^(2(n-1))=2^(10)\\\\2^(2n-2)=2^(10)`

so we see that the bases are equal, that must mean the exponents are equal

`2n-2=10\\\\2n=10+2\\\\2n=12\\\\n=6`

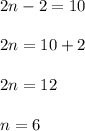
so there are 6 terms