The general form of a solution of the differential equation is already provided for us:
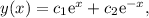
where
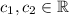 . We now want to find a solution
. We now want to find a solution
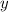 such that
such that
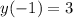 and
and
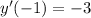 . Therefore, all we need to do is find the constants
. Therefore, all we need to do is find the constants
 and
and
 that satisfy the initial conditions. For the first condition, we have:
that satisfy the initial conditions. For the first condition, we have:
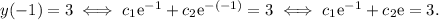
For the second condition, we need to find the derivative
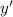 first. In this case, we have:
first. In this case, we have:
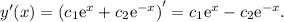
Therefore:
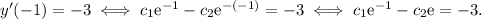
This means that we must solve the following system of equations:
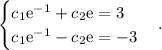
If we add the equations above, we get:
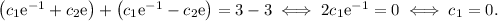
If we now substitute
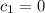 into either of the equations in the system, we get:
into either of the equations in the system, we get:
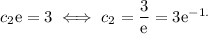
This means that the solution obeying the initial conditions is:
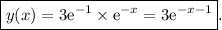
Indeed, we can see that:
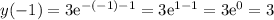
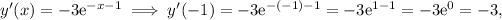
which do correspond to the desired initial conditions.