Which equation below is TRUE? (2^(5) )^(5) = 2^(10) (1)/(10^(2) ) = 10^(-2) 1^(0)=0\\

Question

Which equation below is TRUE?


`(2^(5) )^(5) = 2^(10)`

`(1)/(10^(2) ) = 10^(-2)`

`1^(0)=0\\`

Answer 1

1/10² = 10⁻²

Explanation:

Option 1 : (2⁵)⁵

• Rule is when a power applied to a term of an existing power, they are multiplied
• Therefore, (2⁵)⁵ = 2²⁵
• 2²⁵ ≠ 2¹⁰ ⇒ False

Option 2 : 1/10²

• A power in the denominator becomes negative when brought to the numerator
• ⇒ 1/10² = 10⁻²
• 10⁻² = 10⁻² ⇒ True

Option 3 : 1⁰

• Any number raised to the power 0 is equal to 1
• 1⁰ = 1
• 1 ≠ 0 ⇒ False

Answer 2

`\huge\boxed{\bf\:(1)/(10^(2)) = 10^(-2)}`

Explanation:

Let's check all the equations.

`\rule{150pt}{2pt}`

`1^(0) = 0`

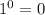
We know that, any number with 0 as its exponent will be equal to 1. Hence, this equation is incorrect.

`\rule{150pt}{2pt}`

`(2^(5))^(5) = 2^(10)`

Let's solve the left hand side of the equation first.

`(2^(5))^(5)\\= 2^(5*5)\\= 2^(25)`

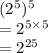
We can see from this that,

`2^(25) \\eq 2^(10)`

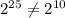
Since, the left hand side
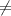`\\eq` right hand side, this equation is also false.

`\rule{150pt}{2pt}`

`(1)/(10^(2)) = 10^(-2)`

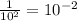
According to the identity ⟶
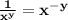`\bf\:(1)/(x^(y)) = x^(-y)`, we can infer that the given equation is correct.

`\rule{150pt}{2pt}`

So, the correct equation is
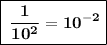`\boxed{\bf\:(1)/(10^(2)) = 10^(-2)}`.

`\rule{150pt}{2pt}`