Answer:

Explanation:
Give that:
the surface equation is

from the family of traces in x = n given that
 , the equation can be represented as :
, the equation can be represented as :
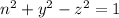

This represents a family of hyperbola for all values of n expects that n = ± 1
So, if n = ± 1,
Then
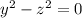
(y-z) (y+z) = 0
y = ± z
So, for n = ± 1, it is a pair of line for y = z, y = -z