Answer:
Domain:
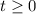
Range:

Explanation:
Given
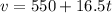
Required
Determine the domain and the range
Solving for domain:
From the question, we understand that t represent years.
Because years can't be negative;
Then, we can conclude that the domain, t is:
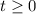
Solving for Range:
We solved domain to be
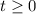
This implies that the minimum value of t is
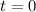 and the maximum is infinity
and the maximum is infinity
Substitute 0 for t in
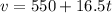
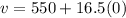

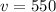
Hence;
The range is
