Answer:
![v = 250[1 - {e^(-6000t)}]](https://img.qammunity.org/2021/formulas/engineering/college/98iliatpp9ov8tbjf9sku9q6wqygzpqbfe.png) mV
mV
Step-by-step explanation:
The voltage across a capacitor at a time t, is given by:
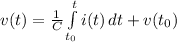 ----------------(i)
----------------(i)
Where;
v(t) = voltage at time t
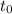 = initial time
= initial time
C = capacitance of the capacitor
i(t) = current through the capacitor at time t
v(t₀) = voltage at initial time.
From the question:
C = 2μF = 2 x 10⁻⁶F
i(t) = 3
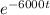 mA
mA
t₀ = 0
v(t₀ = 0) = 0
Substitute these values into equation (i) as follows;
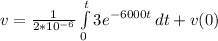
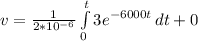
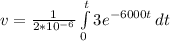
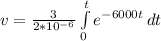 [Solve the integral]
[Solve the integral]
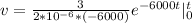
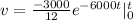
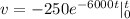
![v = -250 {e^(-6000t)} - [-250 {e^(-6000(0))]](https://img.qammunity.org/2021/formulas/engineering/college/h097i9va2tzq2cdxtxcupuca46xisn2wxp.png)
![v = -250 {e^(-6000t)} - [-250]](https://img.qammunity.org/2021/formulas/engineering/college/qz5bm1ruk06xtl9s9mgse8wszpu43nbo2z.png)
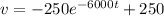
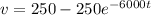
![v = 250[1 - {e^(-6000t)}]](https://img.qammunity.org/2021/formulas/engineering/college/98iliatpp9ov8tbjf9sku9q6wqygzpqbfe.png)
Therefore, the voltage across the capacitor is
![v = 250[1 - {e^(-6000t)}]](https://img.qammunity.org/2021/formulas/engineering/college/98iliatpp9ov8tbjf9sku9q6wqygzpqbfe.png) mV
mV