Question

The two main components ofa stereo system are a radio and a speaker (ignore all other components). The lifetime of the radio is exponentially distributed with mean of 1000 hours and the lifetime of the speaker is exponentially distributed with mean of 500 hours, independent of theradio’s lifetime. What is the probability that system’s failure is due to the radio?

Answer 1

the probability that system’s failure is due to the radio =
`(1)/(3)`

Explanation:

From the question given;

Let the mean lifetime of the radio
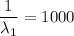`(1)/(\lambda_1) = 1000` and the mean lifetime of the speaker
`(1)/(\lambda_2) = 500`

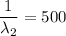
we can re-write both expressions as:

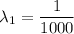`\lambda_1= (1)/(1000)` and
`\lambda_2= (1)/(500)`

Let consider
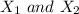`X_1 \ and \ X_2` to be the variables which are independent to the exponentially distributed mean of
`(1)/(\lambda _1) \ and \ (1)/(\lambda _2)`

∴

`P(X_1< X_2) = \int ^(\infty)_(0) \ P (X_1<X_2|X_1 =x) \lambda_1 e^(-\lambda_1 \ x) \ dx`

`P(X_1< X_2) = \int ^(\infty)_(0) \ P (X_1<X_2) \lambda_1 e^(-\lambda_1 \ x) \ dx`

`P(X_1< X_2) = \int ^(\infty)_(0) \ e^(-\lambda_2 \ x) \lambda _1 \ e^(-\lambda_1 \ x) \ dx`

`P(X_1< X_2) = \int ^(\infty)_(0) \lambda _1 \ e^((-\lambda_1 +\lambda_2)) \ dx`

`P(X_1< X_2) = (\lambda_1)/(\lambda_1 + \lambda_2)`

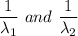
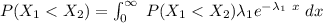
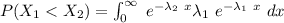
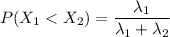
replace the values now; we have:

`P(X_1< X_2) = ((1)/(1000) )/((1)/(1000) + (1)/(500))`

`P(X_1< X_2) = ((1)/(1000) )/((1+2)/(1000) )`

`P(X_1< X_2) = ((1)/(1000) )/((3)/(1000) )`

`P(X_1< X_2) = {(1)/(1000) } * {(1000)/(3)`

`P(X_1< X_2) = {(1)/(3) }`

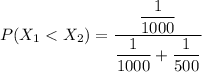
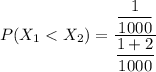
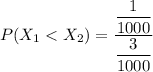
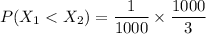
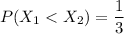
Thus, the probability that system’s failure is due to the radio =
`(1)/(3)`