Question

The department of transportation in a particular city knows from past records that 27% of workers in the downtown district use the subway system each day to commute to and from work. The department suspects that this proportion has increased owing to decreased parking spaces in the downtown district. A random sample of 130 workers in the downtown district showed that 49 used the subway daily. Test the claim at the 5% level of significance. What is the value of sample statistics

Answer 1

We conclude that the proportion has increased owing to decreased parking spaces in the downtown district.

Explanation:

We are given that the department of transportation in a particular city knows from past records that 27% of workers in the downtown district use the subway system each day to commute to and from work.

A random sample of 130 workers in the downtown district showed that 49 used the subway daily.

Let p = population proportion of workers in the downtown district use the subway system each day to commute to and from work.

So, Null Hypothesis,
`H_0` :
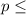`p \leq` 27% {means that the proportion has decreased or remain equal owing to decreased parking spaces in the downtown district}

Alternate Hypothesis,
`H_A` : p > 27% {means that the proportion has increased owing to decreased parking spaces in the downtown district}

The test statistics that will be used here is One-sample z-test statistics for proportions;

T.S. =
`\frac{\hat p-p}{\sqrt{(p(1- p))/(n) } }` ~ N(0,1)

where,
`\bar X` = sample proportion of workers who used the subway daily =
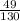`(49)/(130)` = 0.38

n = sample of workers = 130

So, the test statistics =
`\frac{0.38-0.27}{\sqrt{(0.27(1-0.27))/(130) } }`

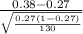
= 2.825

The value of z-test statistics is 2.825.

Now, at a 5% level of significance, the z table gives a critical value of 1.645 for the right-tailed test.

Since the value of our test statistics is more than the critical value of z as 2.825 > 1.645, so we have sufficient evidence to reject our null hypothesis as it will fall in the rejection region.

Therefore, we conclude that the proportion has increased owing to decreased parking spaces in the downtown district.